Modeling in the frequency domain is a crucial concept in control systems, signal processing, and communications. It involves transforming time-domain signals and system behaviors into their frequency components, allowing for easier analysis and design of systems, especially when dealing with oscillatory or periodic signals.
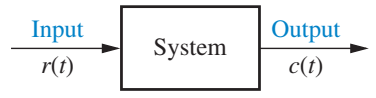
Below fig is of the control system where the input, output, and system are distinct and separate parts.
Below fig is of the control system of cascaded systems:

Laplace Transform
The Laplace transform (F(s)) of a function f(t)is defined as :
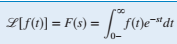
where s = σ + jω, is a complex variable.
Inverse Laplace Transform
The inverse Laplace transform, which allows us to find f(t) for given F(s), is
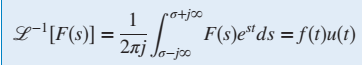
where u(t) is the unit step function i.e u(t)=1 for t>0 and u(t)=0 for t<0.
Laplace transform table

Transfer Function
A transfer function represents the relationship between the output signal of a control system and the input signal, for all possible input values..
Let us write a general nth-order, linear, time-invariant differential equation :
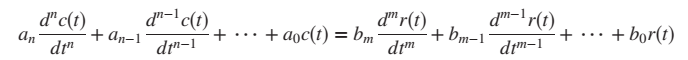
where c(t) is the output, r(t) is the input, and the ai, bi , and the form of the differential equation represent the system.
If we take Laplace transform both sides and If we assume that all initial conditions are zero, the above equation becomes :
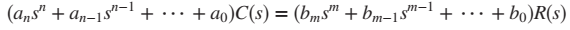
The ratio of C(s)/R(s)= G(s) is called the transfer function and we evaluate it with zero initial conditions :
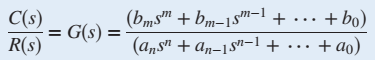
Methods of Obtaining a Transfer Function
There are broadly two ways of obtaining a transfer function for any control system. The ways are following:
Signal Flow Graphs: The modified form of a block diagram is a signal flow graph. Block diagrams visually outline a control system, while signal flow graphs provide a more compact representation.
Block Diagram Method: It is not convenient to derive a complete transfer function for a complex control system. Therefore the transfer function of each element of a control system is represented by a block diagram. Block diagram reduction techniques are applied to obtain the desired transfer function.
Poles and Zeroes of transfer function
Transfer function of a control system can also be represented as
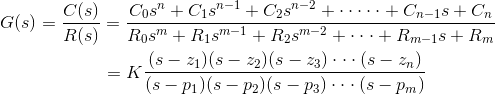
Where K is known as the gain factor of the transfer function.
In the above function if s = z1, or s = z2, or s = z3,….s = zn, the value of transfer function will be zero. These z1, z2, z3,….zn, are roots of the numerator polynomial. As for these roots the numerator polynomial will be zero and the transfer function will also be zero, these roots are called zeros of the transfer function. Zeros affect the steady-state response and how the system reacts to specific frequencies.
For s = p1, or s = p2, or s = p3,….s = pm, the value of transfer function will be infinite. Thus the roots of denominator are called the poles of the function. Poles influence the system’s transient behavior, determining how fast the system responds, whether it oscillates, and if it is stable or not.
By using the transfer function, we can generate Bode plots, which graphically represent the frequency response of the system. Bode plots consist of:
- Magnitude Plot: Shows how the gain (output amplitude) changes with frequency.
- Phase Plot: Shows how the phase of the output signal shifts relative to the input across frequencies.
Bode plots are widely used to assess system stability, design controllers, and filter unwanted frequency components.
Stability Analysis Using Transfer Functions
Stability in control systems is determined by the location of the poles of the transfer function. The Routh-Hurwitz criterion, Nyquist plot, or Bode plot can be used to assess stability in the frequency domain. A system is stable if all poles of the transfer function are in the left half of the s-plane (i.e., they have negative real parts).
Transfer Function in Control System Design
The transfer function is fundamental in designing and tuning controllers such as PID (Proportional-Integral-Derivative) controllers. Using the transfer function, designers can analyze the system’s response to different inputs and adjust controller parameters to meet desired performance metrics, such as rise time, settling time, and overshoot.
Laplace transform in form of Impedance Z(s) is calculated as:

Conclusion
Modeling in the frequency domain is a powerful tool for analyzing systems and signals, especially when dealing with periodic or oscillatory behavior. Techniques like the Fourier and Laplace transforms, along with transfer functions and frequency response plots, enable engineers to design, optimize, and ensure the stability of systems in both control and signal processing applications. Though it may seem abstract compared to time-domain analysis, frequency domain modeling offers unique insights into how systems behave and respond to different inputs.