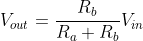Electric Current and Ohm’s Law are fundamental concepts that provide the foundation for understanding electricity.
What is Electric Current?
Electric current is the flow of electric charge through a conductor, typically carried by electrons in a wire. The concept of current is crucial to the functioning of any electrical circuit. It is measured in amperes (A), where one ampere represents the flow of one coulomb of charge per second.
There are two main types of current:
- Direct Current (DC): In DC, the electric charge flows in one direction. Batteries are a common source of DC power, and this type of current is often used in low-voltage applications, such as electronic devices.
- Alternating Current (AC): AC changes direction periodically. The power supplied to homes and businesses is typically AC, as it is more efficient for transmitting electricity over long distances.
Understanding Ohm’s Law
Ohm’s Law is one of the most fundamental laws in electrical engineering, defining the relationship between voltage (V), current (I), and resistance (R). It states that the current flowing through a conductor between two points is directly proportional to the voltage across those two points and inversely proportional to the resistance of the conductor.
The mathematical expression of Ohm’s Law is:
I = V / R
Where:
- I is the current in amperes (A),
- V is the voltage in volts (V),
- R is the resistance in ohms (Ω).
In practical terms, voltage can be compared to water pressure in a pipe. Higher pressure pushes more water through the pipe, just as higher voltage pushes more electrons through a conductor.
Resistance is the opposition to the flow of electric current in a material. It is measured in ohms (Ω). Different materials have different levels of resistance, with conductors like copper offering low resistance and insulators like rubber offering high resistance.
Factors affecting Resistance
The resistance R offered by a conductor depends on the following factors :
R=ρ*L/A (ρ-Resistivity, L-length, A-Area of cross section of conductor)
(i) It varies directly as its length, l.
(ii) It varies inversely as the cross-section A of the conductor.
(iii) It depends on the nature of the material (Resistivity). Unit of resistivity is ohm-metre (Ω-m)
(iv) It also depends on the temperature of the conductor
Effect of Temperature on Resistance
The effect of rise in temperature is :
(i) to increase the resistance of pure metals. The increase is large and fairly regular for normal ranges of temperature. The temperature/resistance graph is a straight line . As would be presently clarified, metals have a positive temperature co-efficient of resistance.
(ii) to increase the resistance of alloys, though in their case, the increase is relatively small and irregular. For some high-resistance alloys like Eureka (60% Cu and 40% Ni) and manganin, the increase in resistance is (or can be made) negligible over a considerable range of temperature.
(iii) to decrease the resistance of electrolytes, insulators (such as paper, rubber, glass, mica etc.) and partial conductors such as carbon. Hence, insulators are said to possess a negative temperature-coefficient of resistance
Rt -R0 = α *R0* t
where Resistance at 0°C is R0 and at t°C is Rt.
and α (alpha) is a constant and is known as the temperature coefficient of resistance of the conductor.
Electrical Power
The electrical power consumed by a circuit is the rate at which energy is used, and it is measured in watts (W). Power can be calculated using the following formula:
P = V × I
Where:
- P is the power in watts (W),
- V is the voltage in volts (V),
- I is the current in amperes (A).
Using Ohm’s Law, we can also express power in terms of resistance and current:
P = I² × R
Or in terms of voltage and resistance:
P = V² / R
These equations are essential for calculating the power requirements of electrical devices and ensuring that circuits are designed to handle the necessary power load.
Voltage Divider Formula
It consists of an electric circuit composed of two resistors and one input voltage supply.
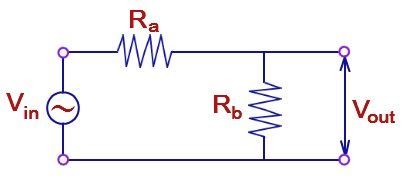
The voltage divider formula is given by :